Play by play: Machine learning exposed

Notas tomadas de un curso de Pluralsight titulado Play by play: machine learning exposed. Los play by play son cursos donde un par de personas trabajan juntas en un proyecto o problema. Normalmente una de ellas es una experta en el tema, y la otra hace de estudiante, aportando una visión novedosa e ingenua del tema.

En este caso, Katharine Beaumont es la experta en machine learning y James Weaver es el novato en el campo, aunque aporta su visión experta en el mundo del desarrollo de software.

Índice del curso:

• Machine Learning Introduction
  • Introduction
  • Supervised Learning Overview
• Supervised Learning
  • Types of Supervised Learning Problems: Regression and Classification
  • Anatomy and Visualizing Artificial Neural Networks
  • Forward Propagation
  • Back Propagation
  • Speed Dating Example
  • Evaluating and Optimizing a Neural Network
  • Regression Sum and Tic-tac-toe Examples
  • Introduction Intuition, K-means Algorithm
  • Using Unsupervised Learning to Map Art and Words
• Reinforcement Learning
  • Using BURLAP, Navigating a Grid World with Q-learning
  • Bellman Equation and Reward Tables
  • Tic-tac-toe with Reinforcement Learning
• Course Conclusion
  • Other Neural Networks Architectures and Conclusion

Glosario

• Regresión lineal
• Gradiente: la velocidad de un cambio, cómo de rápido varía un cambio
• Peso (weight): en este curso se representa con la letra griega theta ( θ )
• Coste: media de la suma de los errores al cuadrado
• Diferenciación: variación de una hipótesis a la siguiente
• Ratio de aprendizaje α: ratio de variación de los pesos θ entre iteraciones
• SoftMax: método de activación de nodos en una red neuronal. Su objetivo es que la suma de todas las activaciones de una capa de nuestra red siempre sume 1. Normaliza las activaciones para que sumen 1
• logistic function: como método de activación de nodos en una red neuronal
• umbral binario: como método de activación de nodos en una red neuronal
• sigmoid activation function: como método de activación de nodos en una red neuronal
• bias: término que permite tener más control sobre la función sigmoide de activación
• Hyperbolic tangent activation function: otro tipo de funciones de activación de los nodos
• Overfitting: tu modelo es muy bueno prediciendo la respuesta para los datos del entrenamiento pero no predicen nada con datos fuera de los de entrenamiento
• Centroide: punto que representará las coordenadas centrales de cada uno de los conjuntos en el algoritmo K-medias

Machine learning introduction

Regresión lineal: lo que queremos saber es la relación que hay entre el tamaño de la vivienda en m^2 y el precio: y = mx + c (y = θ1x + θ2)

Con unos pesos inventados, hacemos una estimación. Ahora necesitamo una forma de saber cómo de buena o mala es dicha estimación.

Cuando hablamos de error, en verdad estamos hablando de diferencia.

Restamos el valor estimado del valor real, elevamos al cuadrado, sumamos y calculamos la media. Este concepto es el coste. El coste nos indica cómo de cerca está nuestra hipótesis (estimación) de los datos. Por lo que si hacemos otra estimación o hipótesis, podremos compararlas. h(x) representa una hipótesis.

Diferenciación es la variación de una hipótesis a la siguiente.

De esta forma, hay un valor para los pesos θ donde el valor del coste es mínimo (que no cero).

Una forma de optimizar los valores de m, c o θs para minimizarel coste es mirar el gradiente de la función coste J:

• Si la función coste J aumenta cuando θ aumenta, en el siguiente paso debemos reducir θ
• Si la función coste J disminuye cuando θ aumenta, en el siguiente paso debemos aumentar θ

Cuando lleguemos a un mínimo, el gradiente será cero, y el coste dejará de variar.

Nota: ¿Recuerdas aquellos problemas de matemáticas donde se buscaba el mínimo de una función haciendo que su primera derivada valiera cero? Pues esto me recuerda a eso

Podemos ir ajustando los valores de θ segun el ratio de aprendizaje, α. α indica cuánto vamos a variar los valores de θ en cada iteración. Este valor de α es un valor que tenemos que decidir/ajustar manualmente.

Por ponerlo en una fórmula:

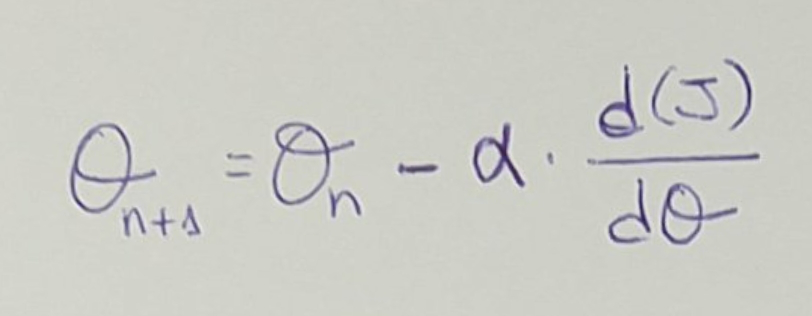
Derivamos la función de coste J por la variación de θ, y dependiendo de ello, así aplicamos el valor de α.

Se puede inicializar θ de forma aleatoria, y se puede realizar todo el proceso varias veces, para intentar conseguir distintos resultados.

Para los casos donde tengamos varias dimensiones, la función de coste no será una simple curva, será una función de 3 o más dimensiones por lo que puede haber mínimos relativos.

A veces, la regresión lineal no es suficientemente buena y necesitas regresión polinomial. En estos casos, hayar el mínimo en el gradiente es más complicado porque hay más variables/dimensiones.

Aprendizaje supervisado (supervised learning)

En este concepto se engloban problemas de regresión (como lo anterior) y de clasificación.

En el curso se centran en un problema de clasificación de flores de iris. Para clasificarlas hay que mirar 4 variables: ancho y largo del pétalo, ancho y largo del sépalo.

En los problemas de clasificación se utilizan las redes neuronales, donde podemos diferenciar varios componentes:

1. Capa de entrada (input layer), donde tenemos tantas entradas como características (features) vamos a manejar. Para el caso de la flor de iris, 4 características.
2. Capa de salida (output layer), donde tendremos tantos nodos como clasificaciones. Si hay 2 especies de flores de iris, tendremos 2. Si hay 3, tendremos 3…
3. Capas ocultas (hidden layers), son las capas intermedias. Estas capas, en realidad, están modelando características que no están explícitamente o directamente creadas por nosotros. Trabaja con algo basado en lo que nosotros le decimos, pero no sabemos exactamente el significado de sus resultados. Estas capas representan características ocultas.
4. Pesos (weights), son similares a los pesos en las regresiones lineales, y son la forma de relacionar nodos de una capa con los nodos de la capa siguiente.

En redes neuronales, θ representa cuánto valor de la característica de entrada pasa al siguiente nodo.

Existe el concepto de activación de nodo o activación de la neurona. Hay diferentes formas de activación: SoftMax, logistic function, umbral binario, sigmoid activation function,…

Entrenar una red neuronal es realizar los cálculos necesarios para hallar los valores de θ de las capas ocultas.

Propagación hacia adelante (fordward propagation)

Bias es un término que permite tener más control sobre la función sigmoide de activación. Hace que la función se active más pronto o más tarde.

Los pesos, θ, es lo que intentamos calcular (igual que en el caso de la regresión lineal). Simplemente, usamos los pesos hallados en la iteración anterior para movernos hacia adelante por la red, para movernos un paso más desde la capa de entrada hacia la capa de salida.

El proceso es el siguiente: se decide cuantas capas ocultas va a tener nuestra red, cuantos nodos va a tener cada una de estas capas y cuantas salidas tendrá nuestra capa de salida. Luego elegimos aleatoriamente los valores iniciales de θ (como en la regresión). Después alimentamos la red con unos valores de entrada y avanzamos por la red, usando los valores de los pesos θ, para que al final del proceso podamos calcular el coste J.

Una vez hecha esta propagación hacia adelante, tenemos que averiguar cómo calcular el coste J. El cálculo de este coste no es muy parecido al visto para la regresión. El cálculo depende de cómo se activan cada uno de los nodos.

Hay un curso online de Stanford donde hablan de ello y de la función logística sigmoide de regresión. En el curso de estas notas simplemente recomiendan usar lo que tu librería de machine learning te proporcione. Me suena muy triste, pero es así.

Propagación hacia atrás (backward propagation)

Una vez calculado el coste J, nos movemos hacia atrás. Vamos entrenando los pesos θ, comenzando por las salias hacia atrás. Comenzamos por el error obtenido y vamos averiguando cómo debemos modificar los pesos θ para que vayamos teniendo una red entrenada para que nos dé buenas predicciones para nuevas entradas.

En este viaje hacia atrás, lo que hacemos es buscar mínimos en la función de coste.

En el caso de las redes neuronales, el gradiente descendente no es tan fácil de calcular. Para regresión lineal teníamos 2 dimensiones, 2 θs. En una red neuronal podemos tener 9 dimensiones para un caso muy sencillo de red. Simplemente representar esa función es imposible. Imagina cómo será buscar el mínimo de dicha función gráficamente.

Al igual que antes, con la función de coste, la búsqueda de este mínimo mediante el gradiente descendente es mejor usar los métodos proporcionados por nuestra librería de machine learning favorita.

Conceptualmente sigue siendo muy parecido a la regresión lineal. Aquí también tenemos el concepto de α, el ratio de cambio de los pesos θ.

Normalmente se necesitan varias iteraciones (hacia adelante y hacia atrás). Es posible que se necesiten miles de ellas. Depende mucho de las capas ocultas. Cuantas más capas ocultas haya, más nodos habrá, más características ocultas habrá, por lo que más dimensiones tendremos que tener en cuenta.

Evaluando y optimizando una red neuronal

Es bastante usual que no se use el 100% de los datos para entrenar la red. Se puede usar el 65% para entrenarla, y el 35% restante para comprobar cómo de bien está entrenado el modelo, aunque estos porcentajes los puedes tomar como quieras.

Overfitting: tu modelo es muy bueno prediciendo la respuesta para los datos del entrenamiento pero no predicen nada con datos fuera de los de entrenamiento. Esto quiere decir que has entrenado tu hipótesis para ajustarse a tus datos, no para generalizar.

El problema opuesto es underfitting: cuando el modelo no se ajusta ni siquiera a los datos de entrenamiento. Puede ocurrir cuando no se está usando el método adecuado.

Además de la función de coste J, que te dice el error que tienes en tus datos de entrenamiento, debes analizar cuánto se equivoca el modelo con los otros datos que tienes. Sería como una función de coste pero para datos que no han sido utilizados en el entrenamiento de la red.

A parte de saber cuántas respuestas son correctas, tú también quieres saber qué tipo de respuestas son las equivocadas. Así, tenemos dos nuevos conceptos:

Precisión: de todas las situaciones donde predecimos que la respuesta es positiva, qué fracción de ellas es realmente positiva. Es decir, porcentaje de aciertos.

Recall: de todas las situaciones donde predecimos que la respuesta es positiva, cuántos de ellos se supone que son positivos.

Hmm, no he pillado muy bien la diferencia entre ellas. Debe ser sutil, o no está muy bien explicado. O puede ser que sean el mismo concepto, pero vistos cada uno desde un punto de vista diferente (resultados obtenidos Vs resultados esperados).

F score: es la media de la precisión y el recall. Sólo será alto si tanto precisión como recall son altos.

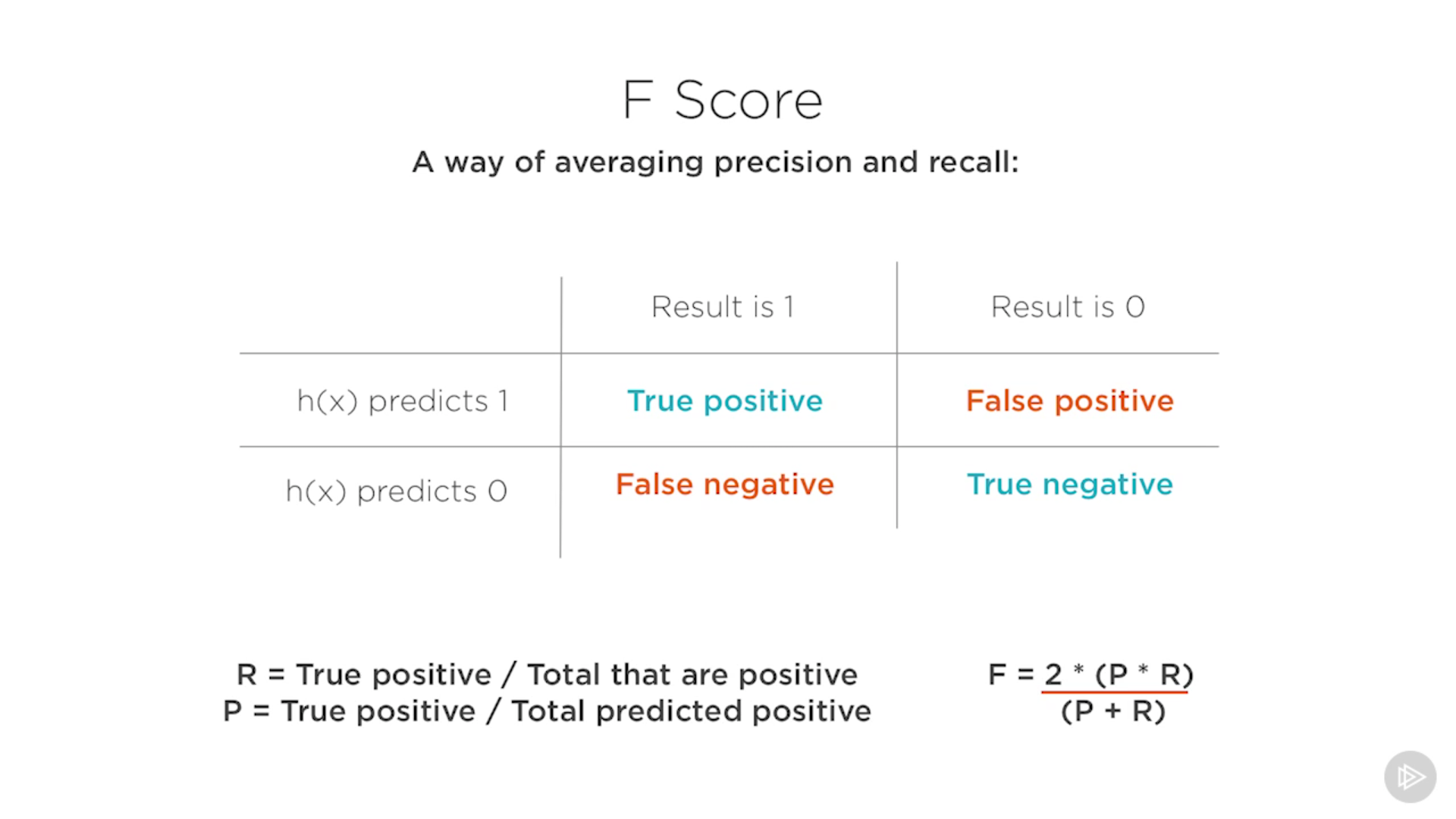
Hay muchas maneras de afectar la salida de una red neuronal. Por eso es bueno conocer cómo medir la red. Para ello tenemos la precisión, el recall, F score, funciones de coste (hay varios métodos para calcularlas: cross entropy, SoftMax,…).

Así podemos hablar de tunear la red, modificando el ratio de aprendizaje, usando más ejemplos para entrenar el modelo, características más pequeñas, o más generales, quizá hayas tomado características que no son tan relevantes como creías, o has pasado algunas por alto, incrementar la regularización de la codificación,…

Algunos autores como VV Preetham dice que tunear una red es un arte oculto. Yo no lo creo, yo creo que estos autores quieren ocultar que en realidad no entienden lo que hacen o que simplemente quieren darle importancia a su trabajo, que desde mi punto de vista de desconocimiento, simplemente parece como que modifican números aleatoriamente.

Ejemplos: suma regresiva y 3 en raya

Normalmente, con una red neuronal hacemos predicciones del resultado que dará para unos datos con los que nunca se han alimentado a la red. Pero en el caso del juego de las 3 en raya, la red ha sido alimentada con todos los movimientos posibles del juego, por lo que al final la red es básicamente unas funciones de aproximación.

Algoritmo K-medias

Antes de nada, como diseñadores del algoritmo, debemos escoger K clusters, es decir, el algoritmo va a clasificar los datos en K conjuntos.

Digamos que queremos 2 conjuntos. Para ello elegimos 2 centroides. Un centroide es un punto que representará las coordenadas centrales de cada uno de los conjuntos. En un principio, las coordenadas de cada centroide son elegidas al azar.

Después nos encontramos con el paso llamado asignación de cluster: para cada dato individual que tenemos, medimos la distancia a cada uno de los centroides, y asignamos el dato al centroide más cercano.

Luego está el paso mover cluster o mover centroide: calculamos dónde está el punto medio de todos los puntos/datos que pertenecen a cada uno de los clusters. Ese punto medio será en nuevo centroide del cluster.

Así, para la siguiente iteración, movemos los centroides a ese punto medio calculado. Y volvemos a hacer el paso de asignación de cluster. E iteramos.

Puede que no sepas con cuántos clusters debes empezar. El número K se considera un hiperparámetro.

El coste en este algoritmo se calcula como la suma de las distancias al cuadrado. Curiosamente, así es como se calcula el error o la distancia que hay de un punto a una recta. Acuérdate de geometría.

Usar aprendizaje no-supervisado para mapear arte y palabras

Hablan de algunos algoritmos más avanzados, y de sus lindezas, pero no entran mucho en detalles y parece más que intentan vender el tema del machine learning.

Aprendizaje de refuerzo

O en inglés reinforcement learning. Es la idea de que el algoritmo tiene un agente que va aprendiendo en base a recompensas. Ejemplos clásicos de estos aprendizajes son un una cuadrícula, donde hay un ratón que se va moviendo por un laberinto hasta que consigue llegar al queso.

La idea es que el ratón, el agente, no sabe nada del mundo, no sabe nada de la cuadrícula. Todo lo que sabe es en qué fila/columna se encuentra, que se puede mover a la izquierda,… y la recompensa que obtiene al moverse.

Supuestamente, el agente de forma aleatoria encuentra el camino hasta el estado final, la recompensa final. Pero sólo por casualidad. Esto es para hacernos una idea de lo aleatorio del algoritmo, y de que realmente el agente no sabe nada sobre la forma del alberinto.

Lo que pasa es que cuanto más cerca está de la recompensa, más directamente va hacia ella. Cuanto más cerca está, más probable es de que consiga la recompensa.

¿Cómo aprende? A través de lo que se conoce como procesos de decisión de Markov. Este algoritmo es una representación de estados, acciones, y en nuestro caso, de recompensas.

Supongamos que el agente se encuentra en la fila 1, columna 2. Puede tomar una acción: moverse arriba, izq… El agente le indica al entorno, al mundo, qué acción va a tomar. Esta acción es un parámetro de entrada del entorno. Así, el entorno calcula qué recompensa va a tener el agente y su nuevo estado. Esta interacción agente-entorno se conoce como SARS (state, action, reward, state).

Existe algo llamado factor de descuento. Ajustándolo, podemos hacer que el algoritmo prefiera recompensas inmediatas o recompensas a más largo plazo. Este parámetro (¿sería un hiperparámetro?) hace que el agente se comporte distinto y aprenda distinto.

Una vez que el agente ha encontrado el camino, se puede volver a iterar. Aquí podemos usar los mismos parámetros o cambiarlos. Podemos decidir si el agente explorará nuevos caminos, porque a lo mejor hay caminos mejores. Este problema se conoce como el problema de exploración versus explotación.

Ecuación de Bellman y tablas de recompensas

Lo que se intenta hacer es asignar un valor para cada posible ación desde un estado.

Hablando de Bellman, una política es una solución. Una política óptima es la mejor acción posible en cada estado. Podemos averiguar la relación entre un paso y el siguiente comparando la función de valor (creo que le llama Q, del término Q-learning) del paso actual con la función de valor del paso siguiente. Usando recursividad, podemos calcular la política óptima del problema.

Tabla de recompensas: indica qué posibles acciones puede tomar el agente dado un estado.

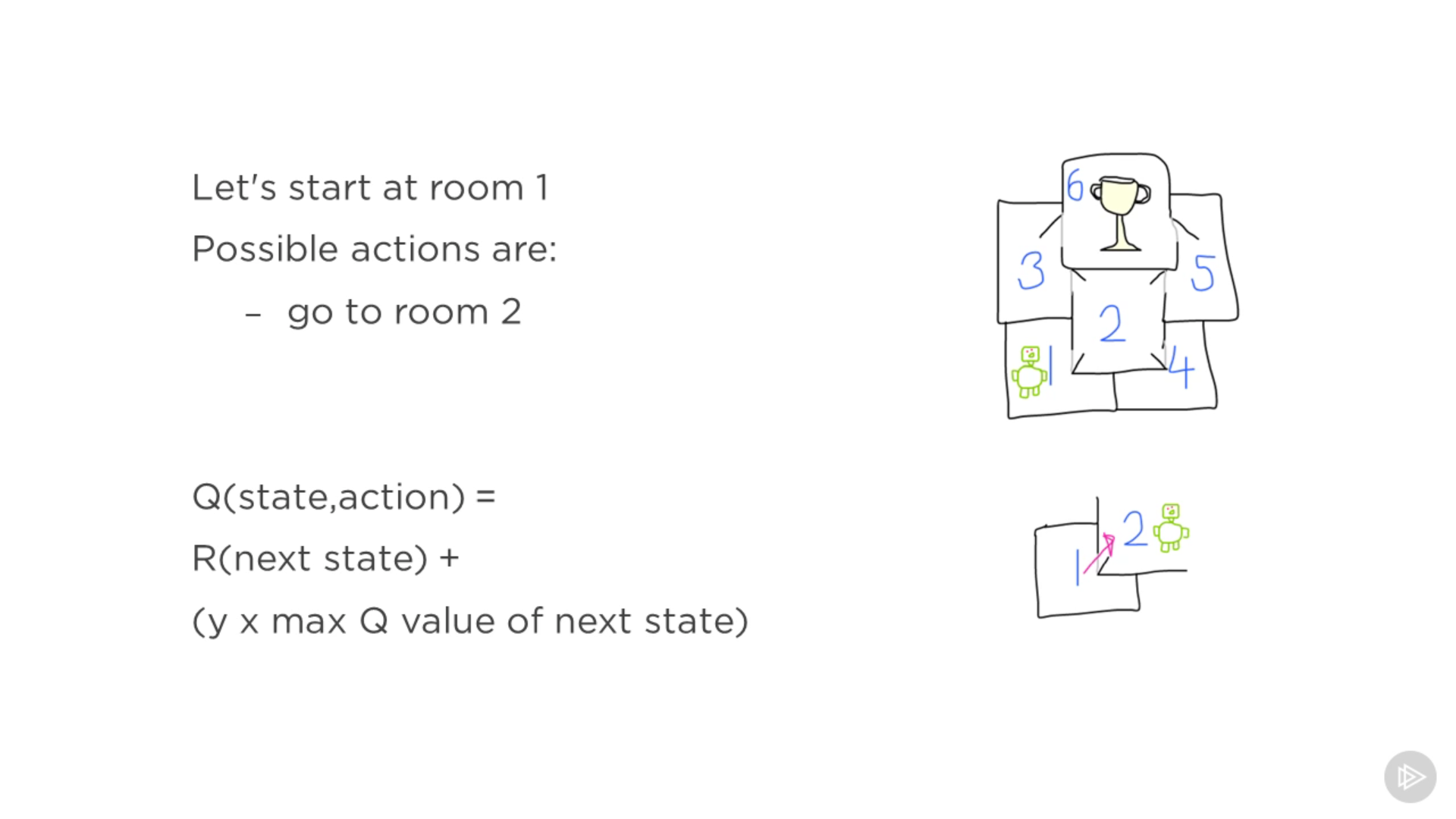
Q(state, action) representa como unas coordenadas en la tabla. Lo que quiero calcular es el valor de ir de la habitación 1 a la 2. Puedo mirar la recompensa R que voy a obtener al moverme a ese siguiente estado (habitación 2) más el máximo valor del siguiente estado multiplicado por el factor de descuento. Este factor de descuento enfatiza más las recompensas cuanto más cerca del estado objetivo se encuentra el agente.

3 en raya con aprendizaje reforzado

La tabla Q representa todos los posibles estados en el juego 3 en raya. Pero no tenemos por qué conocer todos los estados de antemano, los vamos conociendo según nos los vamos encontrando, y así vamos construyendo la tabla (esto sería como ir grabando las partidas para encontrar todas las posibles soluciones).

Necesitaremos varios juegos para construir la tabla completa. Luego, podemos permitir al agente decidir cómo va a maximizar la recompensa según tome unas acciones u otras.

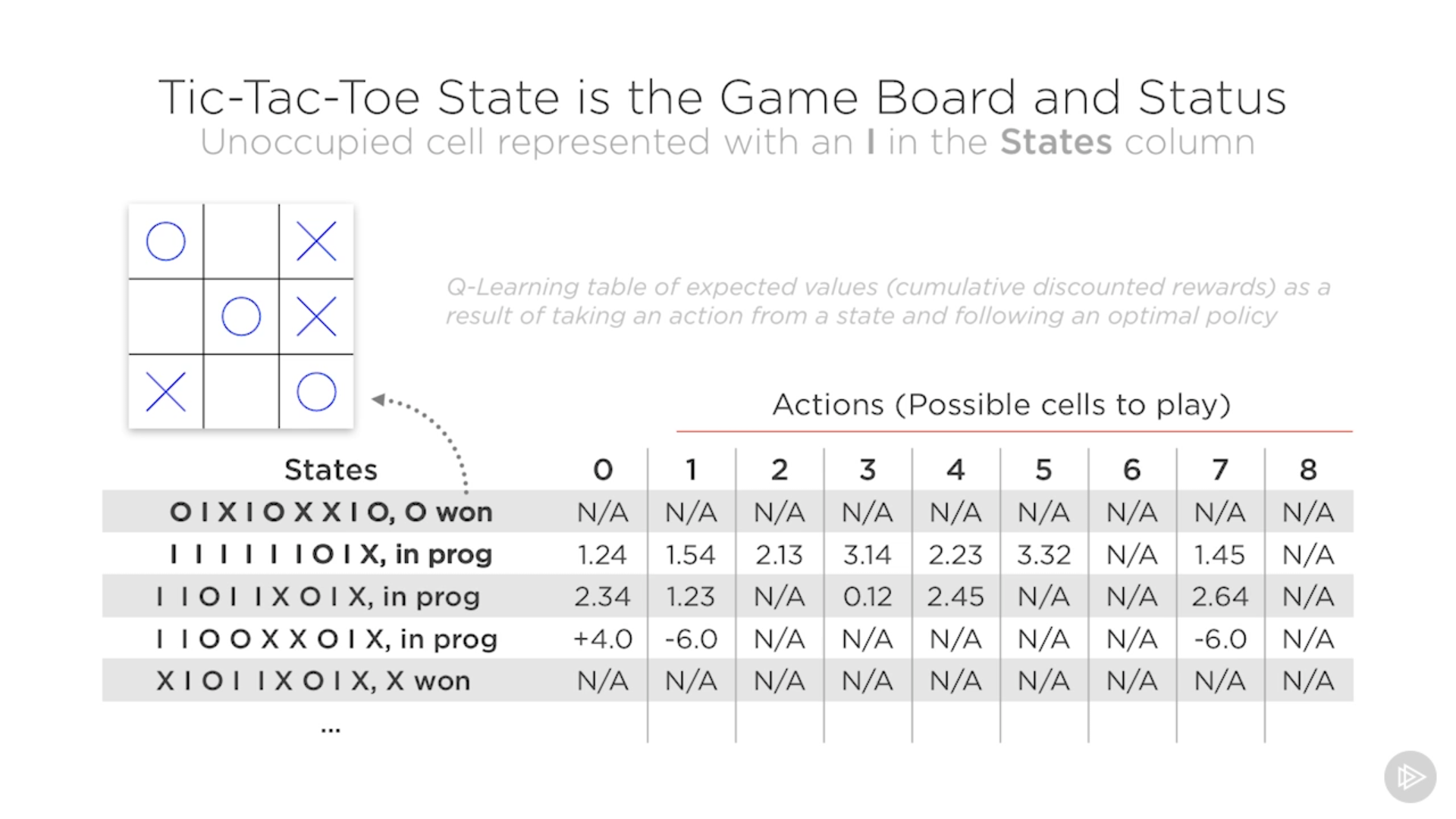
No he pillado muy bien lo de reinforcement learning ¿El entorno tiene almacenado por nosotros las recompensas? Si es así, sería como hacer trampas. Y si no es así… ¿de dónde salen las recompensas? ¿cómo las calcula?

Cierre del curso

Hay más algoritmos o redes neuronales:

• Convolutional neural networks
• MNIST como ejemplo de conditional neural network
• Generative adversarial networks, donde se generan imágenes u otras cosas que no existen todavía